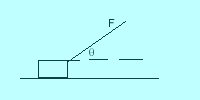
where W is the work, F is the force acting in the direction of the displacement, d
Here is an example of a situation where a force is applied and no work is done: A man holds a 50 N weight. No work is done (even though he must exert a force to hold the weight) because there is no displacement parallel to the direction of the weight.
Here is an example of a situation where there is a force applied and there is displacement and no work is done against the object's weight: A man walks around the room holding a 50 N weight. The object's weight acts down. For work to be done against the weight there has to be displacement in the direction of the weight (either up or down). There is none so no work is done against the weight. There is work done against friction as the man walks around the room.