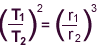In projectile motion, the horizontal and the vertical components of the motion are treated separately. A projectile moves both horizontally and vertically. Its horizontal motion is constant. Its vertical motion is affected by the acceleration due to gravity. The only variable shared by both types of motion is time. Every point on the trajectory is the vector sum of the horizontal and the vertical components of the velocity.
Speed
An object projected horizontally (projected perfectly parallel to the surface) will reach the ground in the same time as an object dropped vertically. Since speed at any point in a trajectory is the vector sum of the horizontal and vertical velocity components at that point, the projected object will have a greater speed when it strikes.
The maximum range for a given initial velocity is obtained when the angle of projection is 45°.
Equations that are used to describe the horizontal and vertical motion:
- horizontal motion (constant velocity):
- d = v t
- where v is the horizontal velocity component and d is the horizontal distance (range)
- vertical motion (acceleration):
- d = vit + ½ a t2
- vf = vi + a t
- vf2 = vi2 + 2 a d
where d is the vertical distance, vi is the initial vertical velocity, and vf is the final vertical velocity
- d = v t
Directions
Advanced calculations
- If horizontal distance is known: Use the horizontal velocity component to calculate time in the air to that point in the trajectory. Substitute in the general equation of motion and solve for vertical displacement, knowing initial vertical velocity component.
- If vertical displacement is known (remember it is positive when measured from the ground "up" to the point in the trajectory): Use the general equation of motion to solve for time to that point in the trajectory knowing initial vertical velocity component.
- Calculate the total time the object is in the air by using the general equation of motion and the initial vertical velocity component. Remember, when the object "hits" the ground, its vertical displacement is zero.
We will be working two types of problems.
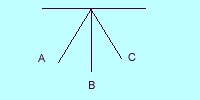
- The first type of problem involves an object that is thrown or projected
at the top (or apex) of its trajectory (at point B in the picture).
At this point, the vertical velocity is zero. Since it starts at this point,
we let vi = zero. It accelerates vertically downward at a
rate of -9.8 m/s2. We usually use the first acceleration formula
listed to find the time the projectile is in the air. The time that it
travels vertically is the same as it travels horizontally. We can use this
time to determine its horizontal range. Its vertical displacement is given
by distance BD and it is negative. Its horizontal range is given by
distance DC.
- vertical: vi = v sin q
- horizontal: vi = v cos q
In this case, q = 0°. Thus, cos q = 1 and sin q = 0 which makes the initial vertical velocity component equal to zero and the horizontal velocity component equal the the horizontally projected velocity.
Advanced calculations
- Consider this problem: An object rolls down an incline and then off the edge of a cliff. Motion information is given allowing one to calculate to speed and angle with which the object leaves the edge of the cliff. Find the initial vertical and horizontal velocity components at the edge of the cliff. Remember, the object is going down, so the sign of the initial vertical velocity component is negative. If the height of the cliff is known, the time to fall can be calculated using the general equation of motion, the initial vertical velocity component, and the acceleration due to gravity. Once time to fall is known, the horizontal velocity component can be used to calculate the distance the object strikes from the base of the cliff. One can also calculate the vertical velocity component the instant before it strikes the ground. It can be used to determine the speed and angle with which the object strikes the ground (remember, it is the vector sum of the horizontal and vertical velocity components at that point).
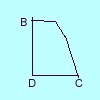
- The second type of problem involes an object that is projected from the ground (point A) and whose path is parabolic. At this point, the speed at which it is projected, v, is the vector sum of its horizontal and its vertical components. At point A, its initial vertical velocity component and its horizontal velocity component are given by:
- vertical: vi = v sin q
- horizontal: vi = v cos q
At pointB, its vertical velocity component is zero. The acceleration at all points is -9.8 m/s2. At point B, the object is accelerating (even though its vertical velocity is zero), because its direction is changing. At all points in the trajectory, the horizontal velocity component remains the same (in the absence of air friction). We will work these problems by finding total time in the air using the second acceleration formula. vf at point C is numerically equal to vi at point A but of the opposite sign. Remember, velocity is a vector quantity! Once we have total time, we can use d = v t to find the horizontal range, knowing that this uses the horizontal velocity componet. We can use the last acceleration formula to predict the maximum vertical displacement (working from points B and D).
- vertical: vi = v sin q
A formula can be derived for the horizontal range:
Advanced calculations
- If horizontal distance is known: Use the horizontal velocity component to calculate time in the air to that point in the trajectory. Substitute in the general equation of motion and solve for vertical displacement, knowing initial vertical velocity component.
- If vertical displacement is known (remember it is positive when measured from the ground "up" to the point in the trajectory): Use the general equation of motion to solve for time to that point in the trajectory knowing initial vertical velocity component.
- Calculate the total time the object is in the air by using the general equation of motion and the initial vertical velocity component. Remember, when the object "hits" the ground, its vertical displacement is zero.
These two types of problems can also be solved graphically using parametric equations on the graphing calculator. If you are interested in learning how to do this, it is explained in the link below.
Graphing calculator solution to problems
One of the classic questions in physics is this: What should a monkey in a tree do when a gun pointed at him fires -- jump down or stay where it is? A graphing calculator solution to this problem is found at Monkey and Hunter Problem
- simple harmonic motion
periodic motion where the unbalanced force varies directly with the displacement from the equilibrium point; this motion is described by the period, the frequency, and the amplitude of the motion- period (T)
the time in seconds needed to complete one cycle of motion- amplitude
the distance from the equilibrium point to the point of greatest displacement- frequency
the number of vibrations in a time interval; its SI unit is hertz (Hz)I like to use the Greek letter, n, as the symbol for frequency. This can be confusing to students since its appearance is similar to the letter v. It can also be represented using the symbol f
- period (T)
- 1 Hz = 1 sec-1
- T = 1/n or T = 1/f
- n = 1/T or f = 1/T
characteristics of a simple pendulum:
- period is independent of mass
- period is directly proportional to the square root of its length
- period is indirectly proportional to the square root of the acceleration due to gravity
- period is independent of amplitude if the arc is less than 10°
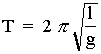
For a pendulum, speed is zero and acceleration is a maximum at the point of maximum displacement (point A). For a pendulum, speed is a maximum and acceleration is zero at the equilibrium point (point B).
acceleration involves a change in speed and/or direction; it is caused by an unbalanced force
in circular motion, the object moves at constant speed but is accelerating because its direction is constantly changing
Uniform Circular Motion
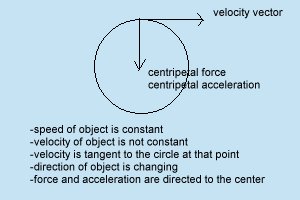
centripetal acceleration:
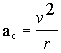
centripetal force:
![]()
You can use your graphing calculator to determine how the magnitude of the centripetal force varies the speed with which the object is swung in the horizontal circle, the mass of the object, or the radius of the horizontal circle.
Banking Angle
Kepler's Laws of Planetary Motion